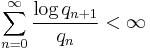Brjuno number

In mathematics, a Brjuno number is an irrational number α such that

$\sum_{n=0}^\infty \frac{\log q_{n%2B1}}{q_n} <\infty$

where p_n/q_n are the convergents of the continued fraction expansion of α. They were introduced by Brjuno (1971), who showed that germs of holomorphic functions with linear part e^2πiα are linearizable if α is a Brjuno number. Yoccoz (1995) showed that this condition is also necessary for quadratic polynomials. For other germs the question is still open.

Brjuno function

The real Brjuno function B(x) is defined for irrational x and satisfies

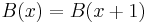
$B(x) =B(x%2B1)$

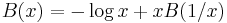$B(x) = - \log x %2BxB(1/x)$ for all irrational x between 0 and 1.

References

Brjuno, A. D. (1971), "Analytic form of differential equations. I, II", Trudy Moskovskogo Matematičeskogo Obščestva 25: 119–262, ISSN 0134-8663, MR 0377192
Marmi, Stefano; Moussa, Pierre; Yoccoz, Jean-Christophe (2001), "Complex Brjuno functions", Journal of the American Mathematical Society 14 (4): 783–841, doi:10.1090/S0894-0347-01-00371-X, ISSN 0894-0347, MR 1839917
Yoccoz, Jean-Christophe (1995), Théorème de Siegel, nombres de Bruno et polynômes quadratiques, "Petits diviseurs en dimension 1", Astérisque 231: 3–88, ISSN 0303-1179, MR 1367353